คณิตศาสตร์: 2017

วันจันทร์ที่ 24 กรกฎาคม พ.ศ. 2560

ฟังก์ชันกำลังสอง คือ ฟังก์ชันที่อยู่ในรูป y = ax² + bx + c เมื่อ a,b,c เป็นจำนวนจริงใดๆ และ a ≠ 0 ลักษณะของกราฟของฟังก์ชันนี้ขึ้นอยู่กับค่าของ a , b และ c และเมื่อค่าของ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ อ่านเพิ่มเติม

http://thnmath22736.blogspot.com/2013/12/blog-post.html

ฟังก์เชิงเส้น (Linear function)

ตัวอย่างของฟังก์ชันเชิงเส้น ได้แก่

1) y = x

2) y =2x +1

ฟังก์ชัน y = ax + b เมื่อ a = 0 จะได้ฟังก์ชันที่อยู่ในรูป y = b ซึ่งมีชื่อเรียกว่า ฟังก์ชันคงตัว (constant function) กราฟของฟังก์ชันคงตัวจะเป็นเส้นตรงที่ขนานกับแกน X ตัวอย่างของฟังก์ชันคงตัว ได้แก่ อ่านเพิ่มเติม

http://thnmath227655.blogspot.com/2013/12/linear-function-fx-ax-b-ab-r-1-y-x-y-2x.html

ค่าสัมบูรณ์ของจำนวนจริง

ค่าสมบูรณ์ของจำวนจริง a : เมื่อกำหนดให้ a เป็นจำนวนจริงระยะจากจุด 0 ถึงจุดที่แทนที่จำนวนจริง a เขียนแทนด้วย |a|
เช่น |2| หมายถึง ระยะจากจุด 0 ถึงจุดที่แทนจำนวน 2 ซึ่งเท่ากับ 2 หน่วย
|-2| หมายถึง ระยะจุด 0 ถึงจุดที่แทนจำนวน -2 ซึ่งเท่ากับ 2 หน่วย

สรุปเป็นกรณีทั่วไป เมื่อ a เป็นจำนวนจริงใด ๆ ได้ดังนี้
|a| = a เมื่อ a > 0
|a| = a เมื่อ a = 0
|a| = -a เมื่อ a < 0

อ่านเพิ่มเติม

ผลการค้นหารูปภาพสำหรับ ค่าสัมบูรณ์ของจํานวนจริง

http://www.mathmyself.com/M4/P55/230/%E0%B8%84%E0%B9%88%E0%B8%B2%E0%B8%AA%E0%B8%B1%E0%B8%A1%E0%B8%9A%E0%B8%B9%E0%B8%A3%E0%B8%93%E0%B9%8C%E0%B8%82%E0%B8%AD%E0%B8%87%E0%B8%88%E0%B8%B3%E0%B8%99%E0%B8%A7%E0%B8%99%E0%B8%88%E0%B8%A3%E0%B8%B4%E0%B8%87.htm

สมบัติการเท่ากันและการไม่เท่ากัน

การเท่ากันของจำนวนจริง
การเท่ากันของจำนวน เราใช้ “ = ” แทนการเท่ากัน เช่น
1 + 2 = 3 ; 6 x 2 = 12
5 – 3 = 2 ; 24 ÷ 3 = 8

การเท่ากันในระบบจำนวนจริงมีสมบัติพื้นฐาน ดังนี้
1. สมบัติการสะท้อน
ถ้า a เป็นจำนวนจริงใด ๆ แล้ว a = a
เช่น 3 = 3
2. สมบัติการสมมาตร
เมื่อ a และ b เป็นจำนวนจริงใด ๆ ถ้า a = b แล้ว b = a
เช่น ถ้า 3 + 4 = 7 แล้ว 7 = 3 + 4
3. สมบัติการถ่ายทอด
เมื่อ a , b , c เป็นจำนวนจริงใด ๆ ถ้า a = b และ b = c แล้ว a = c
เช่น ถ้า 15 = 5 x 3 และ 5 x 3 = 10 + 5 แล้ว 15 = 10 + 5
4. สมบัติการบวกด้วยจำนวนที่เท่ากัน
เมื่อ a , b , c เป็นจำนวนจริงใด ๆ ถ้า a = b แล้ว a + c = b + c
เช่น ถ้า 9 + 1 = 10 แล้ว ( 9 + 1 ) + 2 = 10 + 2
5. สมบัติการคูณด้วยจำนวนที่เท่ากัน
เมื่อ a , b , c เป็นจำนวนจริงใด ๆ ถ้า a = b แล้ว ac = bc
เช่น ถ้า 18 = 9 x 2 แล้ว 18 x 3 = ( 9 x 2 ) x 3 อ่านเพิ่มเติม ผลการค้นหารูปภาพสำหรับ การไม่เท่ากัน

https://orawanintawong.wordpress.com/%E0%B8%9A%E0%B8%97%E0%B9%80%E0%B8%A3%E0%B8%B5%E0%B8%A2%E0%B8%99/%E0%B8%AB%E0%B8%99%E0%B9%88%E0%B8%A7%E0%B8%A2%E0%B8%97%E0%B8%B5%E0%B9%88-1/%E0%B8%AA%E0%B8%A1%E0%B8%9A%E0%B8%B1%E0%B8%95%E0%B8%B4%E0%B8%81%E0%B8%B2%E0%B8%A3%E0%B9%80%E0%B8%97%E0%B9%88%E0%B8%B2%E0%B8%81%E0%B8%B1%E0%B8%99%E0%B9%81%E0%B8%A5%E0%B8%B0%E0%B8%81%E0%B8%B2%E0%B8%A3/

จำนวนจริง

.1จำนวนจริง

เซตของจำนวนจริงประกอบด้วยสับเซตที่สำคัญ ได้แก่

- เซตของจำนวนนับ/ เซตของจำนวนเต็มบวก เขียนแทนด้วย I

I = {1,2,3…}

- เซตของจำนวนเต็มลบ เขียนแทนด้วย I

- เซตของจำนวนเต็ม เขียนแทนด้วย I

I = { …,-3,-2,-1,0,1,2,3…}

- เซตของจำนวนตรรกยะ : เซตของจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วน โดยที่ a,b เป็นจำนวนเต็ม และ b = 0 อ่านเพิ่มเติม

https://sites.google.com/site/khnitsastrm4/bth-thi-4-canwncring

การให้เหตุผลแบบนิรนัย

การให้เหตุผลแบบนิรนัย (Deductive Reasoning)

การให้เหตุผลแบบนิรนัยเป็นการนำความรู้พื้นฐานซึ่งอาจเป็นความเชื่อ ข้อตกลง กฎ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อน และยอมรับว่าเป็นความจริงเพื่อหาเหตุผลนำไปสู่ข้อสรุป เป็นการอ้างเหตุผลที่มีข้อสรุปตามเนื้อหาสาระที่อยู่ภายในขอบเขตของข้ออ้างที่กำหนด

ตัวอย่างที่ 1 เหตุ 1.สัตว์เลี้ยงทุกตัวเป็นสัตว์ไม่ดุร้าย

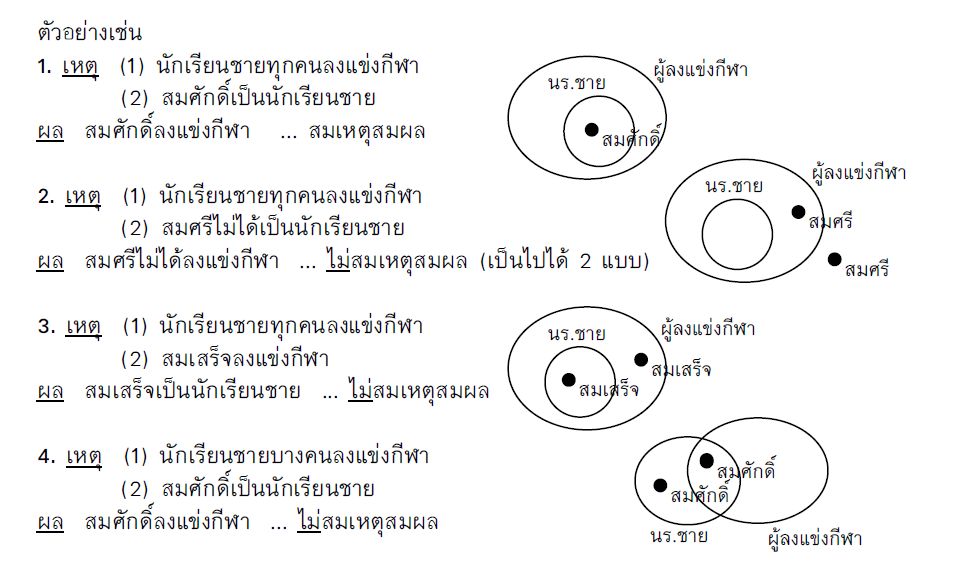
2. แมวทุกตัวเป็นสัตว์เลี้ยง

ผล แมวทุกตัวเป็นสัตว์ไม่ดุร้าย

ตัวอย่างที่ 2 เหตุ 1. นักเรียน ม.4ทุกคนแต่งกายถูกระเบียบ

2. สมชายเป็นนักเรียนชั้น ม.4

ผล สมชายแต่งกายถูกระเบียบ

ตัวอย่างที่ 3 เหตุ 1.วันที่มีฝนตกทั้งวันจะมีท้องฟ้ามืดครึ้มทุกวัน

2. วันนี้ท้องฟ้ามืดครึ้ม

ผล วันนี้ฝนตกทั้งวัน

อ่านเพิ่มเติมhttps://sites.google.com/site/jirapornsringam/kar-hi-hetuphl-baeb-nirnay-deductive-reasoning

ผลการค้นหารูปภาพสำหรับ การให้เหตุผลแบบนิรนัย

การให้เหตุผลแบบอุปนัย

การให้เหตุผลแบบอุปนัย (Inductive Reasoning) เกิดจากการที่มีสมมติฐานกรณีเฉพาะ หรือเหตุย่อยหลายๆ เหตุ เหตุย่อยแต่ละเหตุเป็นอิสระจากกัน มีความสำคัญเท่าๆ กัน และเหตุทั้งหลายเหล่านี้ไม่มีเหตุใดเหตุหนึ่งแสดงให้เห็นถึงความเป็นสมมติฐานกรณีทั่วไป หรือกล่าวได้ว่า การให้เหตุผลแบบอุปนัยคือการนำเหตุย่อยๆ แต่ละเหตุมารวมกัน เพื่อนำไปสู่ผลสรุปเป็นกรณีทั่วไป เช่นตัวอย่างการให้เหตุผลแบบอุปนัย อ่านเพิ่มเติม

https://sites.google.com/site/jubjang2535za/bth-thi-2-kar-hi-hetuphl/1-kar-hi-hetuphl-baeb-xupnay

สับเซต (Subset)

สับเซต (subset) หรือ “เซตย่อย” คือ เซตที่เล็กกว่าหรือเท่ากันกับเซตที่กำหนด โดยต้องใช้สมาชิกร่วมกับเซตที่กำหนดเท่านั้น

…….สัญลักษณ์ที่ใช้แทนประโยค ” A เป็นสับเซตของ B” คือ $A\subset B$ …และจะเกิดขึ้นได้ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A นั้นเป็นสมาชิกของเซต B ด้วย หรือเมื่อ A เป็นเซตว่างก็ได้